double fourier transform proof PDF,Doc ,Images
2 The Fourier Transform
cases the proof of these properties is simple and can be formulated by use of equation 1 so that if we apply the Fourier transform twice to a function ...
Lecture 2: 2D Fourier transforms and applications
Fourier transforms and spatial frequencies in 2D. • Definition and meaning the 1D Fourier analysis with which you are familiar. ... Proof: exercise.
EE 261 - The Fourier Transform and its Applications
4.2 The Right Functions for Fourier Transforms: Rapidly Decreasing Functions . examples you might think of here the function
fpxq a0 fpxq a0e0ix bn
and the formula on the left defines fpxq as the inverse Fourier transform of cp?q. Let's calculate a few basic examples of Fourier transforms:.
Self-reciprocal functions and double Mordell integrals
27 oct. 2021 Although in [11] this identity was proved for b = 0
Lecture 11 The Fourier transform
examples. • the Fourier transform of a unit step. • the Fourier transform of a Examples double-sided exponential: f(t) = e. ?a
The Fourier Transform and Some Applications
4.2 The Double Fourier Transform To prove lim F(a>) = 0 it is sufficient to show that lim [f (t) cos cot dt. <w-»±co ... Integrate by parts twice to get.
On Fourier Transforms and Delta Functions
The Fourier transform of a function (for example a function of time or space) provides a way to analyse the function in terms of its sinusoidal components
[PDF] Lecture 2: 2D Fourier transforms and applications
Fourier transforms and spatial frequencies in 2D Proof: exercise provided the sampling frequency (1/X) exceeds twice the greatest frequency of the
lect
[PDF] 2 The Fourier Transform - School of Physics and Astronomy
cases the proof of these properties is simple and can be formulated by use of so that if we apply the Fourier transform twice to a function, we get a spatially
properties
notes on Fourier transforms - Penn Math
The formula on the right defines the function cpωq as the Fourier transform of fpxq, and the Let's calculate a few basic examples of Fourier transforms: Hermitian) inner product, we have to take the complex conjugate of the second factor,
Fouriertransform
[PDF] 2D Fourier Transform
Examples – A bit of theory • Discrete Fourier Transform (DFT) • Discrete Cosine Second, one has to specify around what point the function is even or odd
matdid
[PDF] 7: Fourier Transforms: Convolution and Parsevals Theorem
Convolution in the time domain is equivalent to multiplication in the frequency domain and vice versa Proof of second line: Given u(t), v(t) and w(t) satisfying
TransformParseval
[PDF] 2 Fourier Transform
3 The function has bounded variation The Fourier transform is linear, since if f(x) and g(x) have Fourier transforms F(
fourier transform
[PDF] 2-D Fourier Transforms - NYU
Fourier Transform for Discrete Time Sequence Examples of 1D Convolution Second pass: find minimum and maximum values of the intermediate image,
lecture DFT
[PDF] Lecture 15 Fourier Transforms (contd)
Proof: By definition, the Fourier transform of h is given by H(ω) = 1 √2π ∫ ∞ Furthermore, the above double integral is separable and may be written as
Fourier
[PDF] The Fourier Transform and Some Applications - CORE
4 2 The Double Fourier Transform 59 and used the function we call the Fourier transform To prove lim F(a>) = 0 it is sufficient to show that lim [f (t) cos cot dt
[PDF] Chapter 5 The Discrete Fourier Transform
The Fourier transform of a sequence F ∈ ΠN is given by ˆ F(m) = 1 N 0, otherwise Note: The complicated proof of this simple method will pay off in a second
chap
![Fourier Series Fourier Transform and their [PDF]](https://i.imgur.com/oRphf2W.jpg "Fourier Series Fourier Transform and their [PDF]")
![PDF) Notes on \](https://upload.wikimedia.org/wikipedia/commons/thumb/f/f6/Onfreq.svg/360px-Onfreq.svg.png "PDF) Notes on \")
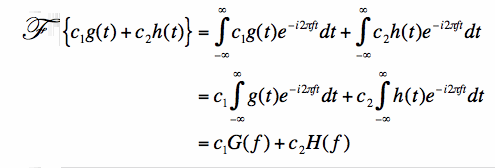
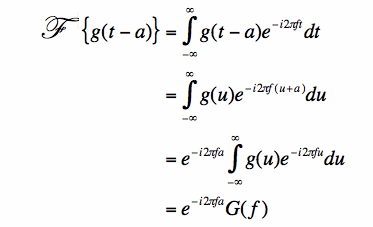
![Fourier Series Fourier Transform and Their [PDF]](https://lpsa.swarthmore.edu/Fourier/Series/Der/Pulse0.2.png "Fourier Series Fourier Transform and Their [PDF]")
